我在初中、高中及大学概率论等相关课程都了解过相关思想,但直到现在我才知道这个具体的名字,故特此记录,也做一个系统总结。
概念简述
蒙特卡罗方法是一种基于随机抽样的统计模拟技术,简单来说就是用随机事件的频率近似概率,用样本均值近似总体期望,从而将确定性问题转化为随机性问题。当使用概率模型模拟结果时,每次都会得到不同的结果。因此在很多实际仿真中会用到该种方法。
数学原理
- 大数定理:当随机抽样次数趋近于∞时,样本均值收敛于总体期望,即:
- 中心极限定理:样本均值的分布近似服从正态分布,可用于误差估计。
工作原理
蒙特卡罗方法建议使用计算机系统来运行足够次数,以产生模拟现实生活结果的不同结果,而系统可以使用随机数生成器来实现输入参数相同但输出结果存在差异的不确定性。
所以,我们可以总结,该方法的组成部分共有三个:输入变量、输出变量及数学模型。
实现步骤
- 分析问题:我们要明确我们的目标是什么,随后我们还要确定在整个过程中的随机变量是什么。
- 随机抽样:生成生成符合指定分布的随机数。
- 模拟实验:代入输入变量,记录输出变量。
- 统计分析:根据目标,选择合适统计量进行计算。
简单举例
近期,我正在学习MATLAB Simulink相关内容,以下是我绘制的信噪比-误码率曲线及其用到的模型:
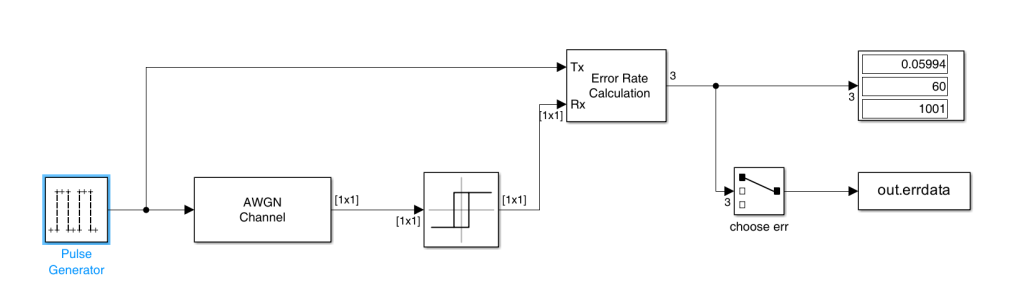
图1 信噪比-误码率仿真模型
相信稍微对相关领域有所了解的人即可看出,这是一个非常简单的模型,由方波生成器生成方波,在AWGN信道传输,经过简单的判决后,计算相关统计量。
其中,我们可以判断出:
- 输入变量:方波
- 输出变量:相关统计量
- 数学模型:AWGN信道,添加高斯白噪声
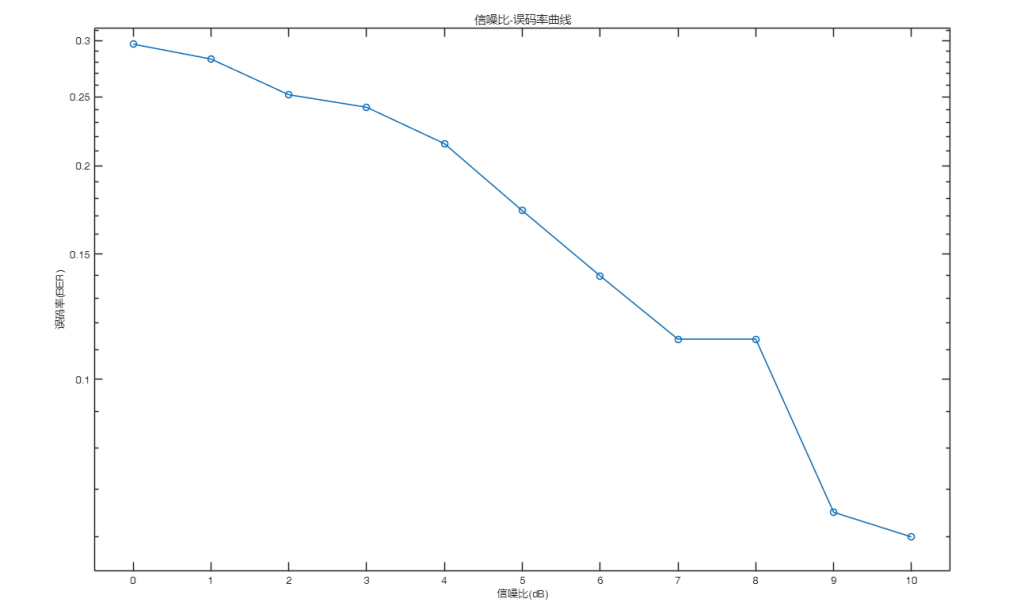
在采样时间为0.01s、仿真时间为10s的条件下,得到相关结果:
图2 信噪比-误码率曲线
总结
蒙特卡罗仿真方法是实际仿真中常用的方法之一,即使用不到相关方法,其思想也成为了我们生活的一部分。
如有问题,欢迎指出。
826字